The field of quantum computing is burgeoning, with a particular emphasis on understanding and utilizing Hamiltonian dynamics in complex systems. Researchers from institutions such as Freie Universität Berlin, the University of Maryland, Google AI, and NIST have made notable strides in enhancing our understanding of bosonic excitations through a newly developed framework for estimating Hamiltonian parameters. Their findings, outlined in a paper on preprint server arXiv, hold the potential to push the boundaries of quantum simulations beyond what classical computers can achieve.
The process of unraveling the intricate details of Hamiltonians—a central concept in quantum mechanics representing the total energy of a system—poses significant challenges. This complexity is heightened in experimental settings where noise, imperfections, and limitations of measurement come into play. The research team, led by Jens Eisert, found themselves confronted with substantial hurdles while attempting to calibrate Google’s Sycamore quantum chip, igniting a collaborative effort toward refining Hamiltonian learning techniques.
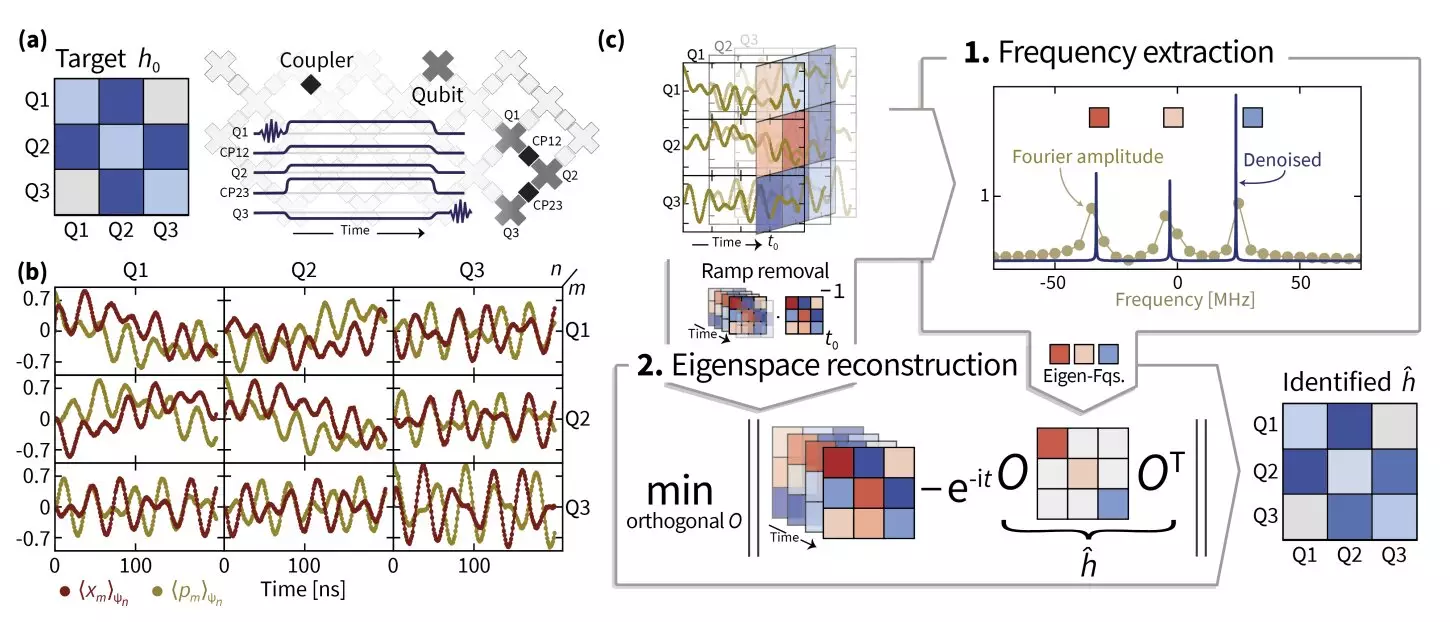
In responding to the initial challenges posed by the Google AI team regarding their superconducting quantum chip, Eisert quickly realized that the intricacies of Hamiltonian learning were far more convoluted than anticipated. Collaborating with adept Ph.D. students, Ingo Roth and Dominik Hangleiter, the team delved into solutions grounded in superresolution methodologies. Through a process marked by trial and error, they navigated difficulties posed by data inaccuracies that obscured effective Hamiltonian identification.
Years of rigorous work culminated in the development of a method known as TensorEsprit, which leverages superresolution techniques to enhance eigenvalue estimation. This new approach, paired with manifold optimization, provided a framework to robustly recover Hamiltonian parameters, significantly improving the reliability of existing methodologies in characterizing complex quantum systems. Unlike traditional approaches relying solely on Euclidean geometries, manifold optimization accounts for the nuances of curved spaces, making it particularly adept at handling the non-linear realities of quantum data.
The implications of these findings are far-reaching. According to Eisert, the ability to extract Hamiltonian parameters precisely even from noisy data could revolutionize how quantum systems are studied and understood. The researchers have shown that their techniques could scale effectively, allowing for robust applications across larger quantum processors. This potential opens avenues not only for enhanced quantum simulation but also for the broader field of quantum technology, which seeks to harness quantum mechanics for practical applications.
One of the pivotal aspects of Eisert’s work lies in its connection to the foundational principles of quantum mechanics. He emphasizes that an accurate understanding of a system’s Hamiltonian is crucial, as predictive power in quantum mechanics hinges on this understanding. As researchers gather data from real experiments, it becomes imperative to stretch the limits of existing theories to include the practical nuances of large-scale quantum interactions.
The research team plans to extend their innovative methodologies to other interacting quantum systems, examining scenarios involving cold atoms—a concept previously explored by physicist Immanuel Bloch. This trajectory not only reiterates the importance of theoretical groundwork in quantum mechanics but also highlights how empirical data can refine and enhance our understanding of these abstract constructs.
Eisert’s assertion that the field of Hamiltonian learning will gain significance in future quantum research encapsulates a critical perspective: understanding fundamental quantum systems’ energy and dynamics is not merely an academic exercise but a necessary step toward more advanced quantum technologies. As quantum computing continues to evolve, the emphasis on refined techniques for Hamiltonian learning will ideally foster breakthroughs in quantum simulations that could have tangible applications in materials science, cryptography, and complex system analysis.
The collaborative efforts among researchers at Freie Universität Berlin, Google AI, and other institutions underscore the critical need for interdisciplinary approaches to tackle the challenges of modern quantum research. Their work on Hamiltonian learning is not simply an academic endeavor; it lays the groundwork for sophisticated quantum simulations that have the potential to revolutionize our understanding of the quantum world.
By addressing fundamental questions regarding Hamiltonians and employing innovative techniques like TensorEsprit, the research team is forging a path toward a more nuanced comprehension of quantum mechanics. As they continue their exploration, the implications of their work could very well redefine how quantum simulators are characterized and understood, ultimately bridging the gap between theoretical physics and practical application.

Leave a Reply