Dynamic systems are complex systems in which a change in one component can have a significant impact on other components. These systems, such as the climate, the human brain, and the electric grid, exhibit nonlinear behavior and undergo dramatic changes over time. Modeling dynamic systems is a challenging task due to their inherent unpredictability. However, in recent years, researchers have turned to machine learning techniques to tackle this problem.
Reservoir computing (RC) is a machine learning approach that has shown promise in modeling high-dimensional chaotic behaviors. It is a simple yet powerful method that involves the use of neural networks. Unlike traditional neural net frameworks, RC is easier and less expensive to train. In 2021, a new variant of RC called next-generation reservoir computing (NGRC) was introduced, which further improved the model’s performance, especially in scenarios with limited training data.
Despite the success and potential of RC and NGRC, researchers Yuanzhao Zhang and Sean Cornelius have identified certain limitations that have been overlooked by the research community. In their study, published in Physical Review Research, Zhang and Cornelius explore these limitations and shed light on a “Catch-22” situation that poses challenges in modeling dynamic systems.
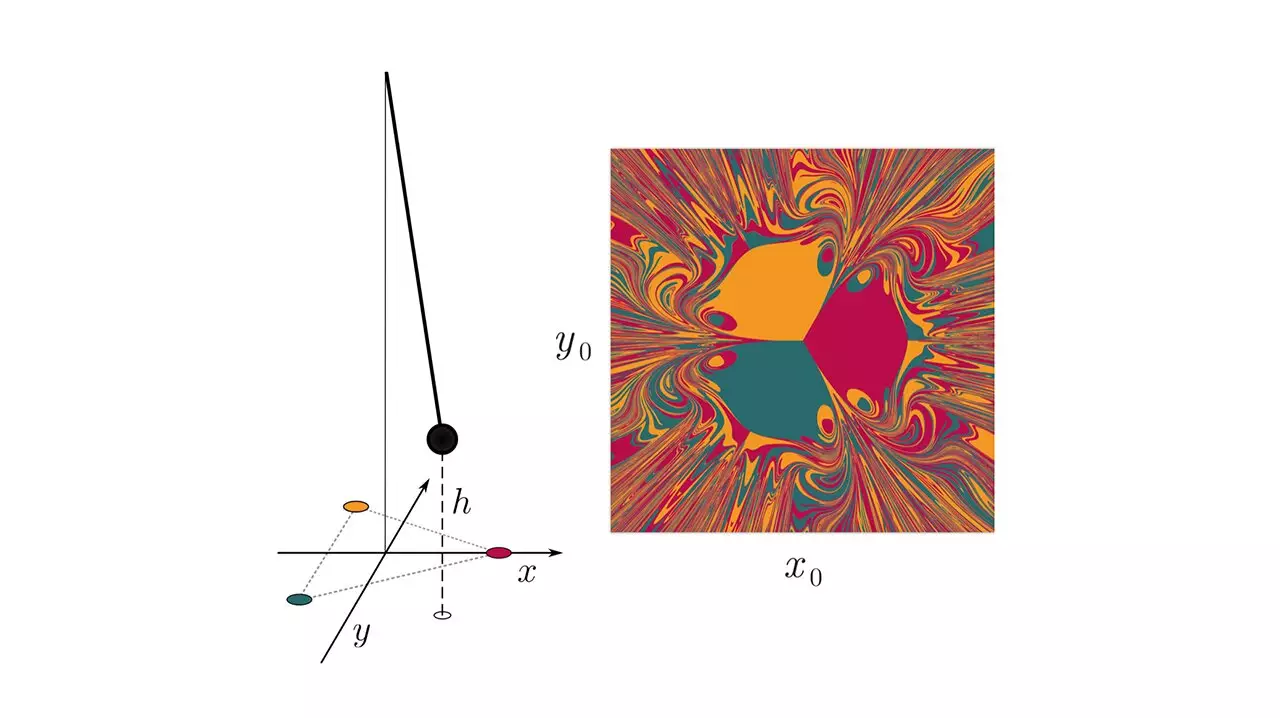
Zhang and Cornelius investigated both RC and NGRC using various dynamic systems. For NGRC, they focused on a simple chaotic system consisting of a pendulum with a magnet attached, swinging among three fixed magnets on a flat surface. The researchers discovered that NGRC performed well when provided with prior information about the nonlinearity of the system. However, when the model was perturbed, its predictive accuracy significantly declined. This suggests that NGRC relies heavily on pre-existing knowledge about the system to make accurate predictions.
In the case of RC, Zhang and Cornelius observed that the model required a lengthy “warm-up” time to correctly predict the system’s behavior. This warm-up time was nearly as time-consuming as the dynamic movements of the magnet itself. This indicates that RC needs extensive training and data before it can accurately model complex dynamic systems.
The limitations identified in both RC and NGRC pose significant challenges for researchers working with dynamic systems. Zhang believes that addressing these limitations is crucial to effectively utilize reservoir computing in modeling complex dynamic systems.
By finding ways to incorporate relevant system information into NGRC models without compromising their predictive performance, researchers can overcome the Catch-22 problem associated with this approach. Additionally, reducing the warm-up time required by RC models can significantly improve their efficiency and applicability in real-world scenarios.
The study by Zhang and Cornelius highlights the need for further research and development in reservoir computing. As scientists continue to explore the potential of this machine learning approach, it is essential to be aware of its limitations and work towards overcoming them. By doing so, researchers can unlock the full power of reservoir computing in modeling and predicting the behavior of complex dynamic systems.
While reservoir computing shows promise in modeling chaotic systems with limited training data, it is crucial to acknowledge and address its limitations. The findings of Zhang and Cornelius shed light on the Catch-22 situation associated with reservoir computing and emphasize the need for further advancements in this field. As researchers continue to refine and innovate in reservoir computing, we can expect more accurate and efficient models for understanding and predicting the behavior of dynamic systems.

Leave a Reply